Introducción
Podemos pensar en las progresivas ampliaciones de los conjuntos numéricos como el
método necesario para resolver ecuaciones algebraicas progresivamente complicadas.
Así,
el paso de N a Z se justificaría por la necesidad de dar solución a una ecuación como
x + 5 = 0
El paso que nos interesa es de R a C viene motivado históricamente por la necesidad de trabajar con las
soluciones de ecuaciones como
x ^ 2 + 1 = 0
La manera más sencilla de trabajar con los números complejos es dar un nombre
abreviado a (√
−1), la llamaremos i.
Hecho eso, ya podemos realizar cálculos como:
Necesitaríamos poder sumar y multiplicar estos nuevos números. Está claro que si
b, c ∈ R, se debiera tener
Por otro lado, para a, b ∈ R no podremos simplificar la expresión a + bi
En primer lugar está claro que si hemos definido i como √
−1,
entonces
i^2 = −1
Si vamos a tener un producto asociativo, conmutativo y distributivo
respecto de la suma, se deberá tener
Con esto ya sabríamos sumar y multiplicar complejos.
Formalización
Una de las formalizaciones es pensar en los complejos como pares (a, b) ∈
R × R con una suma y un producto definidos por
Es un ejercicio sencillo comprobar que la suma y el producto es conmutativa, asociativa, que existe
un elemento neutro.
Decimos entonces que los números
complejos tienen estructura de cuerpo conmutativo..
(a, b) ≡ a + bi.
A estas dos notaciones se las conoce como forma binómica del número
complejo.
Podemos identificar de manera natural un elemento
a de R con el complejo a + 0i = (a, 0). De esta forma podemos considerar R como un
subconjunto de C.
Tendríamos un conjunto destacado de números complejos formado por
aquellos de la forma
bi = 0 + bi = (0, b).
imaginarios puros.
Dado un complejo z = a + bi nos referiremos a a como su parte real y a b como su
parte imaginaria
Interpretación geométrica
Puesto que podemos ver un número complejo como un par (a, b) ∈ R × R, es natural
interpretarlo como un punto del plano. Llamaremos plano complejo al plano R×R cuando
pensamos en él como formado por números complejos. Es claro que en el plano podemos
identificar el eje de abscisas con la recta de los números reales, y el eje de ordenadas con
la recta formada por los números imaginarios puros.
Conjugación
Usar números complejos y que es propia de éstos es la
noción de conjugación. Dado un complejo
Definimos su conjugado z como
Forma módulo-argumental
Si pensamos en un complejo z = a+bi, podemos referirnos a
él de varias formas.
-La primera, con la propia notación binomial.
-Otra forma de describir
ese punto del plano sería decir a qué distancia está el punto del origen y qué ángulo forma
el segmento que une 0 con z con la parte positiva del eje de abscisas.
Llamaremos módulo
de z a la longitud del segmento que une 0 con z, y lo denotaremos como |z|
Utilizando el Teorema de
Pitágoras se tiene
El argumento de un número complejo, denotado Arg(z), es el ángulo
que forma el segmento que une 0 con z con la parte positiva del eje de abscisas, siendo el
sentido positivo para la medida de dicho ángulo, como es habitual, el contrario al de las
agujas del reloj.
Se puede ver que:
Teniendo en cuenta que podemos sumar o restar π al ángulo así obtenido, en
función de los signos de a y b.
Por supuesto, debiera ser posible recuperar la forma binómica del
complejo a partir de su módulo y su argumento. Sea z = a + bi. Llamando ρ = |z| y
θ = Arg(z), se puede ver que.
Esta presentación del complejo es formalmente binomial, pero a la vez deja a
la vista quiénes son el módulo y el argumento de θ.
Las propiedades de las funciones trigonométricas
garantizan que existirá también un entero k tal que θ = α + 2kπ.
Forma exponencial
Merece la pena tener presente este modo de referirse a los números complejos distintos de
0. Apuntamos que comparte
propiedades clave con la función exponencial real y coincide con la exponencial real cuando z = a + 0i es un
número real. Si hubiéramos definido
Para todo par de
números complejos z y w, para z = a + bi tendríamos.
Puesto que a ∈ R,
es su valor habitual. Falta dar sentido a,
Definición: Para todo número real α definimos e^iα como
Una relación tan estrecha entre la función
exponencial y las funciones trigonométricas, queda claro que si z es un complejo de
módulo ρ y argumento θ podemos escribir:
Comprobaremos lo útil que resulta la notación exponencial a la hora de multiplicar y
dividir complejos.
Trigonometría
Para el uso de números complejos es muy importante recordar las diferentes igualdades trigonométricas:
Escribamos
Entonces
De donde se sigue que para multiplicar números complejos en forma módulo argumental,
se multiplican los módulos y se suman los argumentos.
Veamos lo mismo con notación exponencial. En ese caso escribimos
y por
tanto
División
Podemos dividir complejos en forma binomial multiplicando y dividiendo por el conjugado
del divisor:
Pero, si escribimos los complejos como
entonces tenemos la operacion nos llevaria a algo mas complicado m25
por eso nos conviene esto:
-Deducimos que para dividir números complejos en forma módulo argumental, se dividen
los módulos y se restan los argumentos.
De nuevo podemos advertir que la notación exponencial nos permite ahorrar cálculos.
Si escribimos
tenemos:
Potencias
Es fácil darse
cuenta de que calcular potencias en forma binomial no es especialmente eficiente.
Notemos en cambio la siguiente
Fórmula de Moivre. Para todo n ∈ N, para todo θ ∈ R,
Se prueba muy fácilmente usando las fórmulas trigonométricas
Con la fórmula de Moivre a nuestra disposición, tenemos que si
z = r(cos θ + isen θ)
entonces
Por supuesto podiamos haber deducido esto directamente de la formula para el producto de complejos.escribimos:
tenemos:
Cálculo de raíces
En esta sección se muestra que todas las ecuaciones del tipo
Tienen soluciones
complejas. Es claro w^n = 0 posee una única solución,
w = 0.
Sea
Un número complejo, Nos planteamos el
problema de calcular las raíces n-simas de z,
supongamos que
Es una de estas raíces:
es decir w^n = z.
Se tiene que:
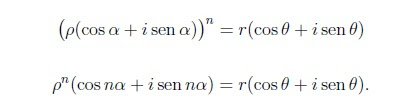De aquí se sigue que para hallar el módulo por así decirlo haríamos lo siguiente:
Por otro lado no se sigue, como podría parecer a primera vista, que nα = θ,
sino, como apuntamos anteriormente, que existe k ∈ Z tal que
nα = θ + 2kπ.
tenemos que:
Eso nos daría en principio infinitas soluciones αk para α, una para cada valor de k.
En realidad, no tenemos infinitas sino exactamente n soluciones para α,
correspondientes a n elecciones consecutivas de números enteros, que den lugar a raíces
n-simas distintas de z.
y observamos que.
Como el argumento de un complejo, da lugar a la misma solución que α0. En consecuencia, existen n raíces distintas das por :
Geométricamente, esto se
traduce en que las raíces n-simas de un complejo z de módulo r están situadas sobre los
vértices de un n-ágono regular inscrito en la circunferencia de radio √n
r con centro en el
origen. 
Lugares Geomètricos en C
Si z = a + b i es cualquier complejo
Es la distancia del origen a z.
Si w = c + d i es otro numero complejo,
entonces:
es la distancia entre z y w en el plano complejo.
Si zo es un número complejo y r es un número positivo, la ecuación
|z − zo| = r
Representa aquellos puntos z cuya distancia a zo es r. El lugar geométrico de los puntos z que satisfacen esta condición es el círculo de radio r con centro en el punto zo.
Si zo es un número complejo y r es un número positivo, la ecuación
|z − zo| < r
Representa aquellos puntos z cuya distancia a zo es menor que
r. El lugar geométrico de los puntos z que satisfacen esta condición es el interior del círculo de radio r con centro en el
punto zo.
Si zo es un número complejo y r es un número positivo, la ecuación
|z − zo| ≤ r
Representa aquellos puntos z cuya distancia a zo es menor o
igual que r. El lugar geométrico de los puntos z que satisfacen
esta condición es el interior del círculo de radio r con centro en
el punto zo incluyendo el círculo mismo
Si z1 y z2 son dos números complejos diferentes, la ecuación
|z − z1| = |z − z2|
Expresa que la distancia de z a z1 es igual a la distancia de z a
z2. Como lo indica, esto significa que z esta en la bisectriz del
segmento que conecta a z1 con z2.
Asì la ecuación
|z − z1| = |z − z2|
Representa la ecuación de tal recta.
Si z1 y z2 son dos números complejos diferentes, la ecuación
|z − z1| < |z − z2|
Expresa que la distancia de z a z1 es menor que la distancia de
z a z2. Como lo indica, esto significa que z esta en el lado
donde esta z1 de la bisectriz del segmento que conecta a z1 con
z2.
Funciones de variable compleja
Recordemos que una función real de variable real sobre un conjunto de números reales es una función que asigna a un número real ∈D otro número real = f(x).
Este concepto se generaliza fácilmente al caso complejo:
Una función compleja de variable compleja definida sobre un conjunto de números complejos es una función que asigna a cada número complejo ∈D otro número complejo = f(z) y la representamos con la notación : D→ℂ.
El conjunto se llama, igual que en el caso de las funciones reales,dominio de . Igualmente, el conjunto de las imágenes de se llama imagen de .
Dado que y = f(z) son de se pueden escribir
= x + yi y = u + vi
(descompuestos en su parte real y su parte imaginaria)
Podemos dar así:
= f(z) = u(x,y) + iv(x,y)
Por tanto, una función compleja = f(z) equivale a tener dos funciones reales y , donde cada una de ellas depende de dos variables reales e .
La representación gráfica de una función compleja utiliza dos planos complejos, uno para el dominio y otro para la imagen; estos dos planos se pueden representar separados o bien superpuestos (en este último caso, se debe diferenciar de alguna manera el valor del dominio y el de la imagen)
Límites y Continuidad de una Función Compleja de Variable Compleja
Sea ƒ: D ⊆ C → C, una función compleja de variable compleja z, definida en la región D ⊆ C excepto posiblemente en Z0 entonces diremos que el límite de f(z) es el número complejo L cuando z se aproxima a Z0 , si y sólo sí, para todo ξ>0, existe un δ>0, tal que:
0< ||z- Z0||< δ, entonces ||f(z) –L||< ξ
Se dice que lim (z)→(z0) f(z) = ∞ si para todo M > 0 existe δ > 0, tal que si |z − z0| < δ entonces |f(z)| > M.
Se dice que lim (z)→∞ f(z) = l si para todo ε > 0 existe N > 0, tal que si |z| > N, entonces |f(z)−l| < ε
Por último, diremos que lim (z)→∞ f(z) = ∞si para todo M > 0 existe N > 0 de manera que ||z| > N, entonces |f(z)| > M.
Los límites de funciones de variable compleja tienen las siguientes propiedades que son análogas a aquellas de los límites de funciones del plano.
(L1) Si el límite existe, entonces es único.
(L2) lim (z)→(z0)f(z) = l si y sólo si lim (z)→(z0) Ref(z) = Rel ylim (z)→(z0) Imf(z) = Iml.
Continuidad de una Función Compleja
Una vez estudiada la noción de límite de una función de variable compleja, pasamos a abordar la continuidad de las misma. Como en el caso real una función f : A ⊆ C → C se dirá continua en z0 ∈ A si existe
- el límite de f(z) cuando z→z0 y
- lim (z)→(z0), f(z) = f(z0).
La función f se dirá continua en A si es continua en todo punto de A.
Como no podía ser de otra manera, la continuidad de f ocurre si y sólo si son continuas la funciones coordenadas Ref e Imf.
Derivadas de Funciones Complejas
Aunque la definición es idéntica en su forma a la derivada real, pues f : A ⊆ C → C se dirá derivable (también holomorfa) en z0 ∈ Int(A) si existe y es finito el límite.
Propiedades de la derivada de funciones complejas:
Ecuaciones de Cauchy Riemann
Si z = x+iy y f(z) = u(x; y)+iv(x; y), y f(z) es analítica en alguna región R en el plano z, entonces las dos ecuaciones:
Conocidas como las ecuaciones de Cauchy-Riemann, se satisfacen en todo R. Las funciones analíticas cumplen con estas ecuaciones.
Funciones armónicas
Las funciones armónicas son aquellas que verifican las ecuaciones de Laplace.
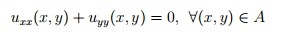
Funciones Trascendentes
En las funciones trascendentes la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
La función logarítmica en base a es la función inversa de la exponencial en base a.
La funciones trigonométricas asocian a cada número real, x, el valor de la razón trigonométrica del ángulo cuya medida en radianes es x.
f(x) = sen x
f(x) = cosen x
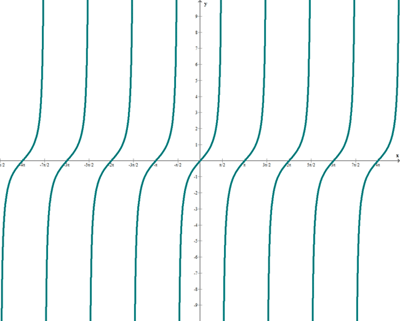
f(x) = tg x
Hiperbólicas
Estas funciones se relacionan entre si mediante reglas muy parecidas a las reglas que relacionan a las funciones coseno y seno. Así como coseno y seno pueden identificarse con el punto (x,y) en el circulo unitario, también las funciones cosh u y senh u. pueden identificarse con las coordenadas de un punto (x,y) sobre la hipérbola unitaria x² - y² =1.
SENO HIPERBÓLICO:
COSENO HIPERBÓLICO:
TANGENTE HIPERBÓLICA
Bibliografía
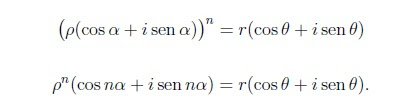
No hay comentarios:
Publicar un comentario