Como se puede observar del mes de Octubre, la revisión del mes llegó hasta la
introducción de las integrales complejas, las mismas que han sido analizadas a
profundidad todo el mes y a continuación se presentan las partes más
importantes en forma de resumen y complementado con material de apoyo de
distintos sitios web:
introducción de las integrales complejas, las mismas que han sido analizadas a
profundidad todo el mes y a continuación se presentan las partes más
importantes en forma de resumen y complementado con material de apoyo de
distintos sitios web:
Como se sabe la variable compleja al ser de la forma z=a+bi; puede ser tratada
como un número único z o como dos variables x+yi. Las integrales de variable
compleja, trabajan con esta propiedad, es decir, que puede ser trabajada como
integral de una variable si se utiliza con un número único z, o como integral de
línea si se tiene la forma x+yi.
como un número único z o como dos variables x+yi. Las integrales de variable
compleja, trabajan con esta propiedad, es decir, que puede ser trabajada como
integral de una variable si se utiliza con un número único z, o como integral de
línea si se tiene la forma x+yi.
Todo esto sugiere que las integrales de variable compleja son solo una aplicación de las integrales de una y dos variables, pero en el caso de los complejos,
existen novedades que solo se definen para este tipo de números tales como las
integrales de Cauchy, y las derivadas de orden superior.
existen novedades que solo se definen para este tipo de números tales como las
integrales de Cauchy, y las derivadas de orden superior.
Tratamiento de una integral si se tiene una única variable z
(Integral indefinida)
(Integral indefinida)
En el caso de que la integral nos pida resolver en función solo de la variable z, se lo definirá en este campítulo como integral indefinida y acudiremos al concepto de integral de una variable, las mismas que su propiedades y formas
de resolución ya se los vio en primer semestre, por lo tanto se se adjuntará un
link muy útil para aclarar conocimientos:
de resolución ya se los vio en primer semestre, por lo tanto se se adjuntará un
link muy útil para aclarar conocimientos:
Curso de integrales en una variable de Roberto Cuadras:
Así mismo se adjunta la imagen
Pero recuerde que a estos resultados se deben sumar la constante c, ya que se
trata de una integral indefinida.
Integrales bajo un intervalo dado (Integrales de variable
compleja definidas)
Analicemos el caso de la integración:
En el mismo no se define la integral indefinida o no tiene una antiderivada
definida en la tabla de la parte superior, por lo tanto aquí se debe establecer
parámetros y uno que otro truco aprendido en cálculo vectorial. Es aquí donde
entra el concepto de integral de línea.
Recuerde que en el campo de los reales la integral de línea se da como dice su
nombre, a través de una línea muy fina y que maneja dos variables (x,y) se
resuelve la misma a través de una parametrización de las variables, bajo un
intervalo establecido por la función y su forma paramétrica. En variable
compleja, este concepto es muy útil, ya que como se sabe en forma triangular a
un número complejo se lo define en la forma z(x,y), por lo tanto el concepto de
integral de línea le viene bien a este tipo de números, pero bajo algunos
conceptos propios, el primero, que la línea fina o delgada cambia de nombre y
se la denomina curva suave o suave por intervalos, geométricamente definidas
de la siguiente forma:
La curva suave es representada con la letra griega gamma Ύ y es representada
como una función de t (paramétrica), es decir z(t)=x(t)+iy(t). Bajo esta
premisa, la condición para que exista una curva suave es que x'(t) y y'(t) son
continuas y que no sean simultáneamente igual a cero.
Propiedades básicas de integración de variable compleja:
- Si Ύ es una curva suave o suave por intervalos y f(z) es continua, entonces se tiene que:
propiedades de la suma, resta y multiplicación por un escalar que las integrales
en una variable.
- Si Ύ es una curva suave o suave por intervalos representada por
z=z(t), para a<=t<=b, y f(z) es continua, entonces:
Estas son las propiedades básicas de la integración de variable compleja. A
continuación se presentarán recursos de apoyo, tales como documentos de
apoyo u ejercicios.
Para que se revise el material de apoyo sobre este tema haga click aquí.
Video que trata la resolución de una integral:
Los ejercicios y material de apoyo de esta parte se presentarán (en su gran
mayoría) al final de la unidad para una mejor revisión de todos los temas.
Conjunto simplemente conexo y simplemente no conexo:
Este concepto no varía de la definición que tenía en cálculo vectorial. Se define
a un conjunto simplemente conexo si todo par de puntos en el dominio D
pueden unirse con un segmento rectilíneo, cuyos puntos pertenecen todos a D.
(Cálculo Vectorial, José Luis Toro, Quito, 1999). Esta propiedad es de suma
importancia para los conceptos que se verán a continuación, su entendimiento
es muy importante.
- Propiedad: sea Ύ una curva suave o suave por partes por intervalos de z1 a z2 en un dominio simplemente conexo. Si f(z) es función analítica, entonces se cumple que:
F'(z) = f(z)
Por lo tanto se cumple en el dominio Dx que:
Integrales Cerradas:
donde: Ύ es una curva suave y cerrada, es decir si el punto inicial y final de la
curva coinciden. Ejemplo: un círculo.
Curva simple en D: Ύ es una curva simple si no presenta entrecruzamientos,
gráficamente esta situación puede ser explicada como:
- Propiedad # 1 de las curvas simples: sea f(z) una función cerrada simple en D.analítica en D, un dominio simplemente conexo y sea Ύ una curva
A esta propiedad se la denomina Integral de Cauchy. A continuación se
presentará un ejercicio con estas características:
- Propiedad # 2 de las curvas simples: si f(z) es analítica en un dominio simplemente conexo D, entonces la integral de línea es independiente de la trayectoria en D.
Para entender de mejor situación esta propiedad, se acudirá a la definición
geométrica de la misma:
- Propiedad # 3 de las curvas simples o Teorema de la deformación: sea f(z) analítica en D, excepto en Zo y sean Ύ y Ω curvas cerradas simples que encierran a Zo. Si es así, se tendrá que:
Geográficamente esta situación puede ser representada como:
Esta propiedad es muy útil cuando no se tiene un conjunto simplemente
conexo, pero que es una integral cerrada; en dicho caso se crea la curva
cerrada Ω que encierre a Zo y se utiliza la propiedad antes mencionada.
- Propiedad 4 (Integrales de Cauchy): si f(z) es analítica en un dominio simplemente conexo D y sea Ύ una curva cerrada simple que encierra a Zo, entonces se puede deducir que:
De esta fórmula es muy fácil deducir un corolario:
- Propiedad 5 (Fórmula de Cauchy para las derivadas de orden superior): sea f(z) analítica en un dominio simplemente conexo D, y sea en Zo, entonces f(z) tiene derivadas de todos los ordenes de Zo, y la n-ésima derivada de f(z) en Zo es:
Donde donde n determina el grado de derivada a tomar en cuenta
De aquí se deriva un corolario:
Ahora se añadirá a más de la teoría dada material de apoyo para la investigación
y observación de como resolver problemas de este tipo:
Una revisión rápida de la teoría explicada: haga click aquí
Una profunda revisión al tema:
Una clase sobre integrales de curvas simples cerradas:
Para una revisión general de ejercicios de cada tema tratado: haga click aquí.
Ejercicios de revisión y aplicación:
Todos los documentos compartidos tienen el total derecho de sus creadores.
SUCESIONES Y SERIES DE VARIABLE COMPLEJA:
En cierta forma, pareciera que se trabaja en una variable, ya que si se puede
hacer una analogía con los temas revisados en Cálculo en una Variable, después
de integrales, se revisaba este tema.
Y de hecho como se dice anteriormente, las sucesiones y series de variable
compleja tienen propiedades similares a las de variable real.
Como este tema se revisó al final de mes, se hará solo una introducción a este tema:
Se pueden considerar a loas principales series como las principales:
- Series de Potencia
- Series de Taylor
- Series de Laurent: esta última es la serie propiamente de los números complejos.
Primero se definirá el concepto de sucesión, la misma que en variable compleja
es una función de los naturales en los complejos.
Una sucesión se denota con la forma {Zn}
Ejemplo:
Ahora se establecerán las propiedades de las sucesiones:
- Sea {Zn} = Xn + iYn, para cada entero positivo "n", y sea L=a+bi,
- Supongase que {Zn} ---> 1 y que {Wn} -->1, entonces se
Hasta ahora, es imposible perderse en el camino, pero...¿Qué pasa si se arma
una serie, es decir una sumatoria de todos los valores de la serie?
Series:
Se define a la serie como una sumatoria de los términos de una sucesión y
matemáticamente tiene la misma definición a través del símbolo Epsilon en
mayúscula.
Ahora el análisis de una serie se da a través de los criterios de convergencia:
Propiedades:
Sea {Zn} = Xn + iYn, entonces:
De estas propiedades se puede crear una lista de series convergentes y
divergentes, las mismas que se pueden observar a través del siguiente
documento y de mejor forma: Haga click aquí
Hasta aquí se ha visto la unidad en el mes de noviembre.
Bibliografía
de http://es.slideshare.net/mariolabestia/ejercicios-resueltos-mm-502
de http://es.slideshare.net/kristhianraul9/integrales-34226483
Molero, salvador, Menarguez, Garmendia . Análisis Matemático , de http://www2.caminos.upm.es/Departamentos/matematicas/Fdistancia/PIE/Analisis%20matematico/Temas/C03_Series_Complejas.pdf
Bombal F. , Sanchéz González . Colección Ejercicios Resueltos, de http://www.ucm.es/data/cont/docs/193-2013-10-17-Ejercicios%202008-2009.pdf

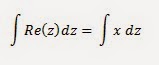

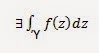
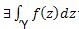

















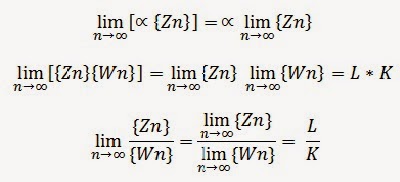


No hay comentarios:
Publicar un comentario